Methods for Conditioning Diffusion Models
A simple overview of different conditioning strategies and their origins
I’ve been spending time on research around different multi-modal generation techniques recently, and was discussing with someone recently about all the different ways you can conditioning diffusion or flow-matching models.
It made me want to make a quick blog post about it, so here you go!
Here is a look at the four conditioning paradigms that define the current landscape of diffusion modeling. There’s obviously more work going on than just these four, but this is what I’ve seen prominently and work effectively. If you have other methods you think are critical to know, mention them below!
1. Early Days: Simple Cross-Attention
The first widely successful approach to conditioning diffusion models came from using cross-attention to merge latent information from different signals, and this was before transformers were the common backbone of diffusion models.
In early latent diffusion systems, the problem was framed very simply: how do you inject a text description into an image denoising process to augment the generation process?
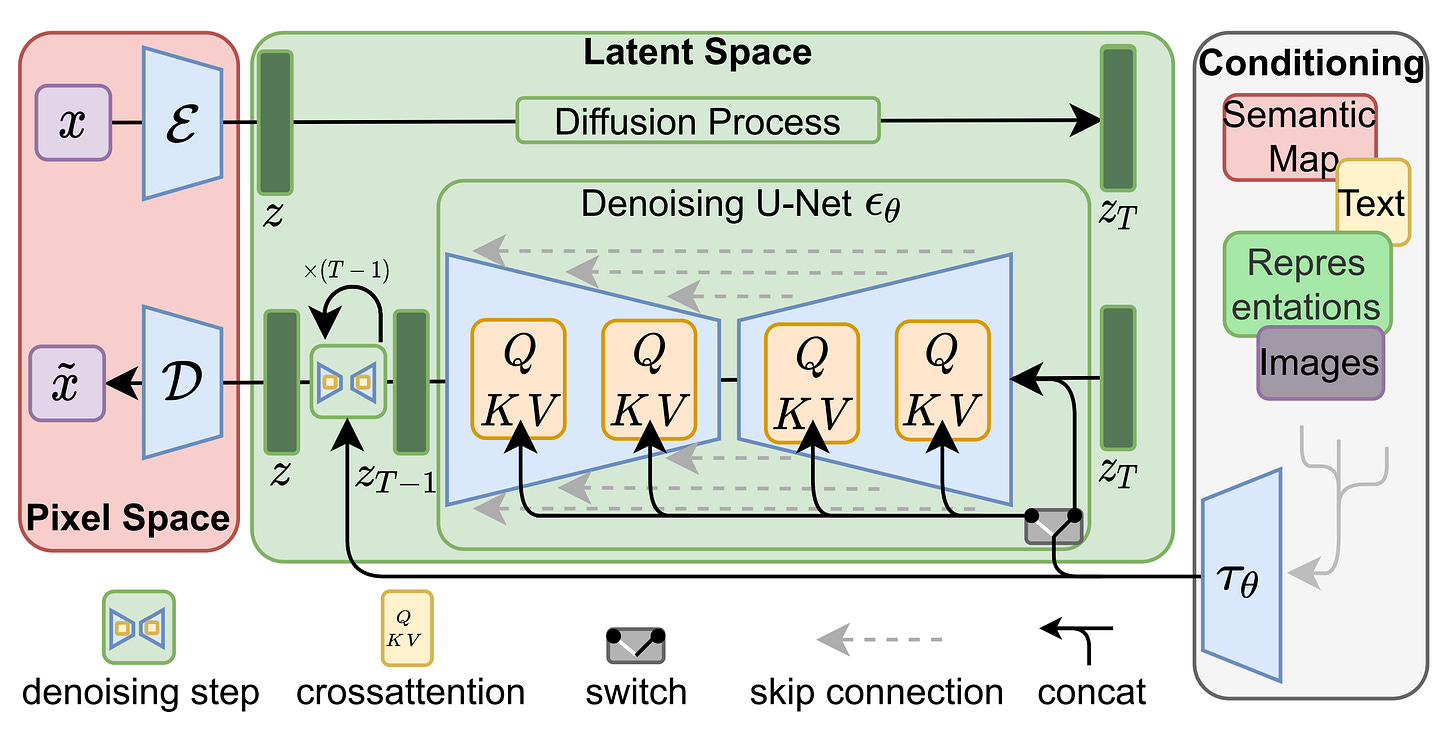
The initial approach that saw success was popularized by High-Resolution Image Synthesis with Latent Diffusion Models (Rombach et al., 2022) from Stable Diffusion 1.5 and beyond. This was to keep the two streams largely separate and connect them through cross-attention.
Text is encoded once by a frozen model such as CLIP, producing a set of keys (K) and values (V). The image latent, evolving through a U-Net backbone during denoising, produces the queries (Q). At each cross-attention layer, the model combines them through a classic attention block:
The cross-attention effectively “injects” conditioning by projecting text embeddings into the image denoiser, where image features act as queries over text-derived keys and values. This mechanism biases the denoising updates toward prompt-consistent semantics while preserving a separation between text representation and spatial image processing.
This design choice was extremely pragmatic and simple. For straightforward text-to-image synthesis, this ended up working remarkably well and defined the baseline for an entire generation of models.
However, the same separation that gives cross-attention its stability also limits its expressiveness. Because text and image representations never fully merge, the model struggles with fine-grained spatial reasoning, compositional logic, and especially typography (remember seeing letters scrambled like they were written schizophrenically?). The conditioning signal is directional and coarse: the text can guide what appears, but not reliably where or how precisely.
2. AdaLN (Adaptive Layernorm): Global Conditioning for Diffusion Transformers
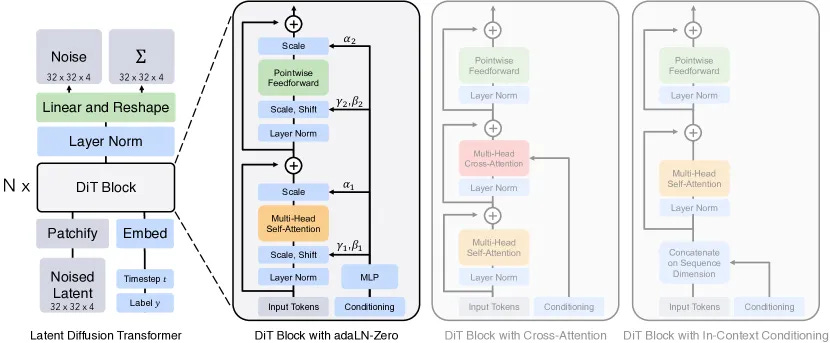
When the paper Scalable Diffusion Models with Transformers (Peebles & Xie, 2022) came out, the field shifted from U-Nets to Diffusion Transformers (DiTs) as the backbones of diffusion models. In this same paper, AdaLN conditioning was introduced, and has really become a preferred method for injecting global context extremely effectively.
The idea is that, rather than adding extra tokens or specialized attention layers, AdaLN modulates the layer normalization blocks. The model learns to predict the scale (γ) and shift (β) parameters of the Layer Normalization based on a condition vector c.
The operation is defined as:
\($AdaLN(x, c) = \gamma(c) \cdot Norm(x) + \beta(c)$\)
This ends up being a really efficient way of applying global conditioning to the diffusion transformer backbone, like adding a time or style conditioning
AdaLN is nice because it’s computationally cheap, O(D) complexity versus the quadratic cost of attention. It influences the entire generation uniformly, making it excellent for setting global style or coherence.
One of the challenges though is is that lacks precision, and it’s edits can be coarse or blunt. It can’t easily tell the model to place a specific object at specific coordinates, or adjust the orientation of that object, etc.
Still, it is one of the most common and powerful ways to apply conditioning to one of these DiT models, and it’s implementation simplicity is quite elegant, making it easy to understand.
Side Note:
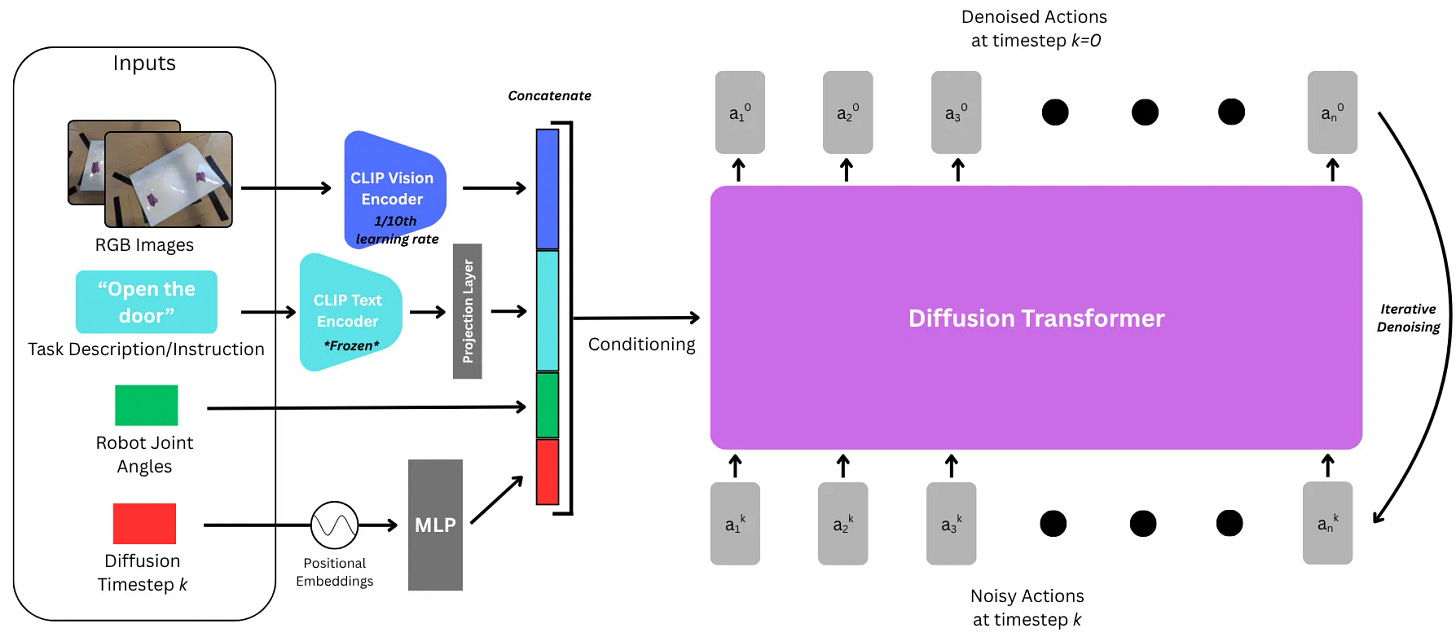
This is one of the most effective ways we’ve seen to condition diffusion and flow matching action chunking policies and -heads for robotics. You take all of your observations, camera view encodings, joint angles, task description, etc, and concatenate them into an AdaLN conditioning vector.
You can see this in action in a repo I’ve open-sourced for Multitask Diffusion Policy, here: https://github.com/brysonjones/multitask_dit_policy/tree/main
3. In-Context Learning (ICL): Few-Shot Adaptation
In-context learning is an approach to apply conditioning in the inputs of the diffusion transformer rather than an architectural modification to inject conditioning during processing.
One of the first papers we saw this with was In-Context Learning Unlocked for Diffusion Models (Wang et al., 2023), where the idea mirrors almost exactly few-shot prompting in LLMs. The model is given one or more example pairs, like an input image and its desired outputs (segmenting, edge detection, style transfer, etc) followed by a new query input.
We end up effectively treating these image tokens as "visual prompts" alongside or instead of text. Just as you might show a language model a few examples of English-to-French translation to teach it the pattern, in diffusion ICL, you feed the model a "context pair" consisting of a source image and a transformed version.
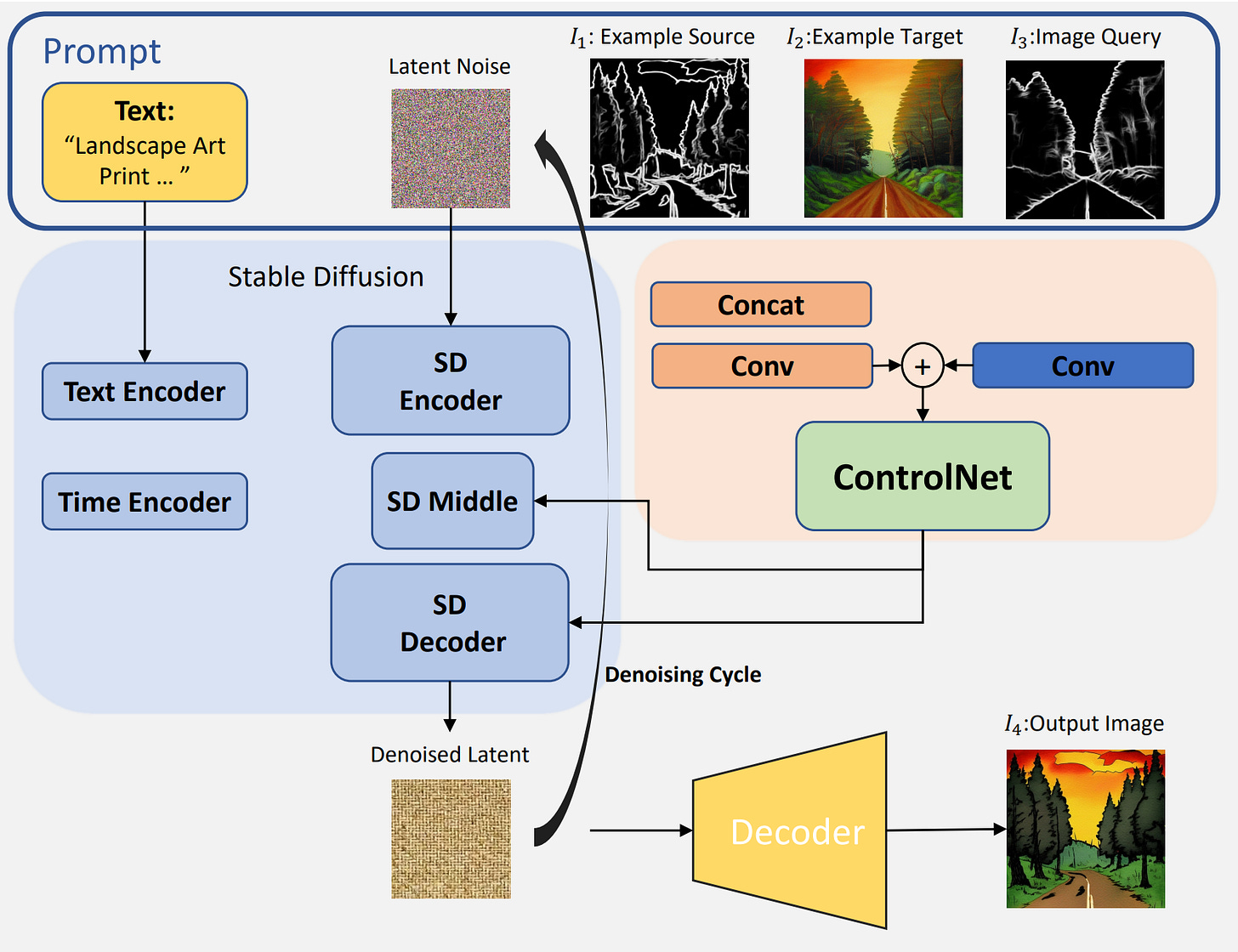
Practically, this is implemented either by concatenating images into a single tensor (for example: stacking an edge map and its target photo next to a new edge map), or by using attention masking so that query tokens can attend to example tokens. The diffusion process implicitly learns the transformation by pattern matching within its context window.
This approach ends up working quite well, and multitask demonstrations end up teaching the model how to combine and generalize these editing concepts. It allows a single pretrained model to perform edge-to-image, colorization, style transfer, and other conditional tasks without specialized adapters.
But this flexibility and expressivity comes at a cost. Because the model is not explicitly optimized for the task, output fidelity usually lags behind fine-tuned or adapter-based methods (this starts to change as you scale, as most models do). Additionally, the approach is fundamentally bounded by context length (quadratic cost on computation) and GPU memory, making it difficult to scale to complex or high-resolution demonstrations.
4. Joint Attention for Multiple Modalities (MM-DiT)
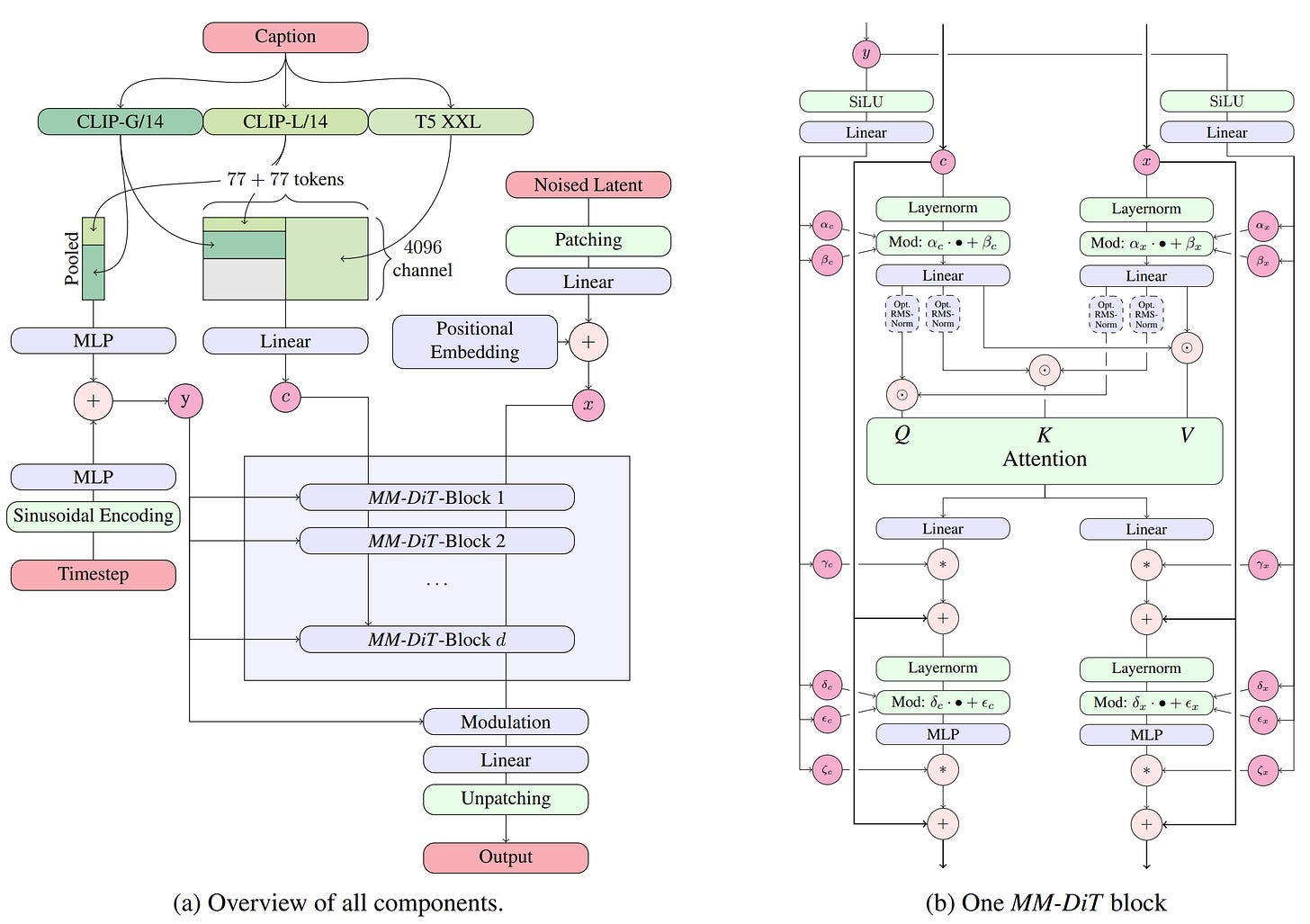
Joint Attention with MM-DiTs represents the one of the most recent big leap in diffusion conditioning. This approach basically creates two separate streams of data that run in parallel through the model layers:
Image Stream: Processes the visual latent patches (the noisy image being denoised).
Text Stream: Processes the text tokens (from the prompt).
Importantly, each stream has its own set of weights. This means the model learns separate parameters to process visual data and textual data, acknowledging that pixels and words behave very differently and have different patterns to learn, etc.
Then within the MM-DiT blocks, image and text tokens are concatenated into a single sequence, processed with attention, and then split back into their distinct streams.
This iterative merging and separation helps ensure the model retains exact character sequences and resolves ambiguity, leading to superior typography (no more misspellings, mangled letters, etc) and complex prompt adherence.
This idea was introduced in Scaling Rectified Flow Transformers for High-Resolution Image Synthesis (Esser et al., 2024) for Stable Diffusion 3. The architecture evolves the simple cross-attention concept into an model that more fully merges the multi-modal signals and you can see the diagram below:
There’s quite a few trade-offs though:
Just like ICL, because we are increasing our input context for these signals, we incur quadratic compute cost increases for increasing context/conditioning length
As you can see from the diagram above, this architecture is quite complicated with lots of sub-details of implementation, making the implementation and hyperparameter tuning cumbersome
There’s a lot of exciting work going on with diffusion/flow-matching generative models right now, and it’s easy to get lost in the sauce of all the different methods. I found trying to group and categorize approaches like this helped me grasp when and where to try and apply the different strategies.
I’m working on diffusion models and other architectures for multi-modal generation, representation learning research, and beyond.
Most of my work is focused on robot manipulation, world-modeling, and decision-making. Reach out if you are interested in chatting (https://x.com/brysonkjones), and share this post with others!